Counting Triangles

Posted on . Updated on .

Update: do not forget to read Counting Triangles (2) after this post.

Some days ago I was watching a movie on TV and I fell asleep just after it finished. When I woke up a couple of hours later it was already the time of participative quizs. These are TV shows in which a game is proposed (usually a very simple game, like a word search) and people call the program to give answers and get a monetary prize. I won’t give much more details about how these shows work and get your money. Yesterday there was, however, a mildly interesting game when I woke up. They presented a geometric figure like the following one:

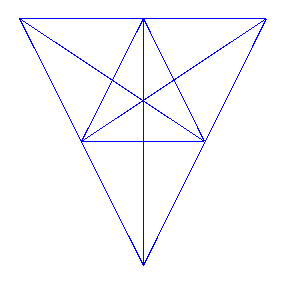
Sample triangle

The goal was to find out the amount triangles present in that image. To ease things from our point of view, we are going to number the vertex.

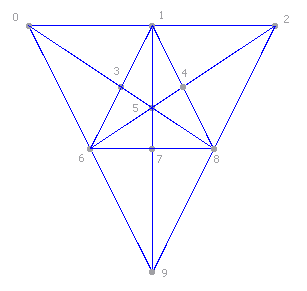
Sample triangle with numbered vertex

Counting the number of triangles by hand is not an easy task at all, and it’s extremely easy to get lost in the process. There is obviously an outside triangle (0, 2, 9), and there are twelve inside triangles formed by one piece each ((0, 1, 3), (1, 2, 4), etc). But there are many more triangles. For example, (1, 6, 8) is also a triangle, and (0, 8, 9) is a valid triangle too. Hopefully, you start to realize how counting the triangles is a very complex process. Just so you get an idea, there are 47 triangles in the sample figure. It looks easy, but it’s not.

This prompted me to try to create a small Python program to count them. It wasn’t difficult at all. I had it running flawlessly in less than 30 minutes. The figure can be understood as a graph from the mathematical point of view, but I’m going to take a simpler approach anybody can understand. The program works with 3 different kinds of elements: vertex, segments and straights.

Vertex

Vertex are just ending points for a segment in the figure. It’s quite simple to understand, because in the second image we numbered the vertex so you can clearly see them. When you are given a figure, the first step is to number each vertex, taking care not to leave any behind.

Segments

A segment is specified as a couple of vertex. Enumerating each segment is the most complex action you need to perform by hand, but compared to counting triangles it’s quite easy. Take the top edge in the figure. In it, we have three vertex called 0, 1 and 2. There are 3 segments in that edge. The obvious segments (0, 1) and (1, 2), but there’s also (0, 2). I’ve come to the conclusion that the easiest method to enumerate segments is to take the vertex in order and see if there’s a straight line that joins it with every vertex of higher index. You start by 0 and see if there’s a line that joins it with 1, 2, …​, 9. You follow by 1 and try to see if there are lines that join it with 2, 3, …​, 9. Etc. In the sample figure above, there are 36 segments, listed below.

0 1
0 2
0 3
0 5
0 6
0 8
0 9
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
2 4
2 5
2 6
2 8
2 9
3 5
3 6
3 8
4 5
4 6
4 8
5 6
5 7
5 8
5 9
6 7
6 8
6 9
7 8
7 9
8 9

Straights

Straights are groups of vertex forming one single line. You can call them lines if you prefer. They are very easy to count. In the sample figure there are 9 straights or lines, listed below.

0 1 2
0 3 5 8
0 6 9
1 3 6
1 4 8
1 5 7 9
2 4 5 6
2 8 9
6 7 8

As you see, the top edge (0, 1, 2) is one of them, but you also have the straight (1, 5, 7, 9) in the middle of the sample figure, etc. Straights play an important part in our program, as you’ll see.

What the program does

The program needs two files as input. The first file is the segments file. Its format is the one I used above, with pairs of vertex, one pair per line. It then needs a second file containing the straights, also in the format I used above. A set of vertex each line, describing one straight each.

The program first proceeds to parse the contents of both files, extracting pairs of numbers and saving them to a set named arches, and the tuples of vertex forming the straights, saving the tuples to a set named straights. The procedure it follows then is very simple.

First, from the segments and straights it forms a list of vertex, and finds the combinations of those elements in groups of 3. Each one of those combinations is a candidate, a possible triangle, that needs to be confirmed. The confirmation comes in two steps. For every combination (a, b, c) it checks if the pairs (a, b), (a, c) and (b, c) are present in the set of segments. Finally, it checks that there are no straights that contain the 3 elements (a, b, c), which would mean that there is no real triangle, but just a straight line. For example, combination (0, 1, 2) is a candidate for which (0, 1), (0, 2) and (1, 2) are segments, as we explained above. However, there is a straight line that contains the elements (0, 1, 2). It is precisely the straight (0, 1, 2). That makes (0, 1, 2) an invalid triangle, because it’s in fact a straight line.

The program finally prints a list of triangles and the total count.

Program code (public domain)

#!/usr/bin/env python
import sys

# Recursive combinations function
def combs_aux(elems, comb_len, depth, start_at, cur_comb, output):
  if depth >= comb_len:
    output.append(tuple(cur_comb))
    return

  for x in xrange(start_at, len(elems) - (comb_len - depth) + 1):
    cur_comb[depth] = elems[x]
    combs_aux(elems, comb_len, depth + 1, x + 1, cur_comb, output)

# Wrapper to ease calls
def combinations(elems, comb_len):
  elems = list(elems)
  output = []
  combs_aux(elems, comb_len, 0, 0, [None] * comb_len, output)
  return output

# Read files
try:
  segments_str = file(sys.argv[1], 'r').read()
  straights_str = file(sys.argv[2], 'r').read()
except (IOError, OSError, IndexError):
  sys.exit('Usage: %s segments_file straights_file' % sys.argv[0])

try:
  segments_lines = [x for x in segments_str.split('\n') if len(x) != 0]
  segments_num_str = [x.split() for x in segments_lines]
  segments = [(long(a), long(b)) for [a, b] in segments_num_str]
except (ValueError, IndexError):
  sys.exit('Error parsing segments file')

# Arches
arches = set()
for seg in segments:
  arches.add(tuple(sorted(seg)))

# Straights
straights_lines = [x for x in straights_str.split('\n') if len(x) != 0]
straights_strlists = [x.split() for x in straights_lines]
straights_lists = [[long(x) for x in lst] for lst in straights_strlists]
straights = set(tuple(sorted(x)) for x in straights_lists if len(x) != 0)

# Extract vertex
vertex = set()
for arch in arches:
  vertex.update(set(arch))
for st in straights:
  vertex.update(set(st))

# Generate combinations and filter them by existing arches and straights
candidates = combinations(vertex, 3)
candidates = [tuple(sorted(x)) for x in candidates]
candidates = [(a, b, c) for (a, b, c) in candidates
    if (a, b) in arches and (b, c) in arches and (a, c) in arches]
triangles = [(a, b, c) for (a, b, c) in candidates
    if len([s for s in straights if a in s and b in s and c in s]) == 0]

# Print triangles and total count
print '\n'.join('(%s, %s, %s)' % (a, b, c) for (a, b, c) in triangles)
print 'Number of triangles: %s' % len(triangles)
Load comments